 |
| Энергетический метод определения критической силы. |
| |
| |
| Ввиду трудности интегрирования дифференциального уравнения
упругой линии стержня часто применяют различные приближенные методы определения
критической силы. Одним из таких методов является энергетический, основанный
на исследовании изменения потенциальной энергии при переходе стержня из
прямолинейной в криволинейную форму равновесия. |
| Поскольку критическим считается то значение сжимающей стержень
силы, при котором равновозможны как прямолинейная, так и бесконечно близкая
к ней криволинейная формы устойчивого равновесия, то согласно рис. 8.4 формы
равновесия I и II равноценны и при переходе из состояния I в состояние II
нет изменения энергии системы в этом случае безразличного равновесия, т.е.
|
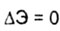 |
| где изменение полной потенциальной энергии системы складывается
из уменьшения потенциала силы Р при переходе из состояния I в состояние
II и приобретения стойкой в состоянии II потенциальной энергии изгиба. Отсюда
|
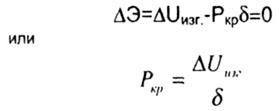 |
| Потенциальная энергия деформаций при изгибе |
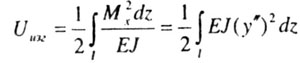 |
| Перемещение точки приложения силы Р |
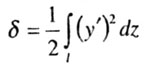 |
| Из этих выражений получаем |
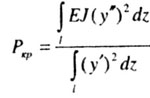 |
| Поскольку в числителе этого выражения - величина, пропорциональная
потенциальной энергии деформаций при изгибе, то интеграл в числителе берется
по всей длине изогнувшегося при потере устойчивости стержня. Если имеются
участки различной жесткости Е, J, то следует взять сумму интегралов по всем
n участкам |
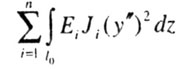 |
| В знаменателе выражения для Ркр
находится величина, пропорциональная перемещению точки приложения нагрузки.
Если на стержень действует несколько продольных сил, то следует умножить
каждую j-ю силу (Рj)
на перемещение точки ее приложения) |
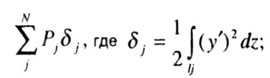 |
| здесь Ij
- расстояние от точки приложения сжимающей силы до нижней опоры, т.е. длина
сжимаемого этой силой участка; N - число I продольных сил. |
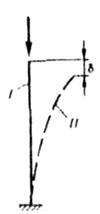 |
| Рис. 8.4 |
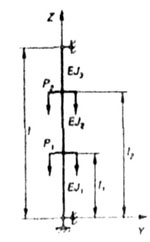 |
| Рис. 8.5 |
| Так, например, для стержня, изображенного на рис. 8.5, баланс
энергии имел бы вид: |
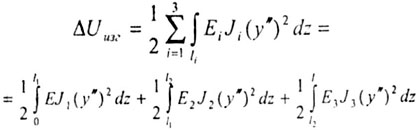 |
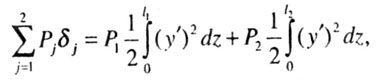 |
| где n - число участков различной жесткости, здесь n = 3. |
| Во всех этих выражениях у = f (z) - функция прогибов, которую
подбираем (поэтому метод приближенный) с учетом граничных условий. Это может
быть, например, тригонометрическое выражение, алгебраическое выражение или
полином, степень которого равна числу граничных условий. Если функция у
= f(z) соответствует истинной форме изогнутой оси, то и решение будет точным. |
| Анализируя граничные условия, следует, изобразив стержень
в деформированном после потери устойчивости состоянии, провести обязательно
оси координат и относительно этих координатных осей продумать, где будут
равны нулю: |
| у - перемещение, |
| уII
- угол поворота оси стержня, |
| уIII
- кривизна, т.е. величина, пропорциональная изгибающему моменту. |
| Последнее граничное условие (по уII
) обычно вызывает наибольшие трудности. Основная идея: поскольку изгибающий
момент пропорционален кривизне оси бруса уII
, то уII
равно нупю там, где равен нулю изгибающий момент, это свободные и шарнирно
опертые концы стержня. |
| Следует обратить внимание на то, что на промежуточной шарнирной
опоре в общем случае уII
# 0 (так как там не равен нулю изгибающий момент). |
| |
 |