 |
| Моменты инерции сечения. |
| |
| |
| Моменты инерции сечения входят в формулы для напряжений и
деформаций. |
| Осевыми моментами инерции сечения
относительно осей X и Y (рис. 4.3) называются определенные интегралы вида |
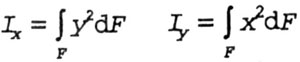 |
| Центробежным моментом инерции сечения
относительно двух взаимно перпендикулярных осей х и y называется определенный
интеграл вида (рис. 4.3) |
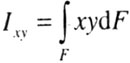 |
| Полярным моментом инерции сечения
относительно начала координат о называется определенный интеграл вида |
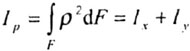 |
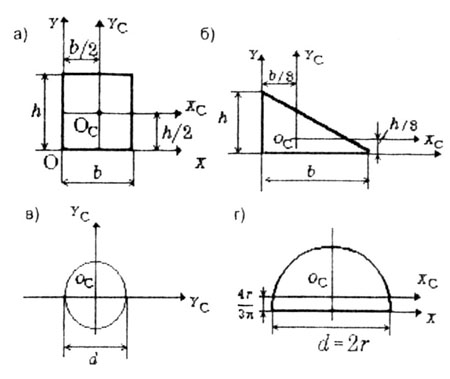
| Ниже приведены моменты инерции наиболее распространенных
простейших сечений: |
| № |
Ixc |
Iyc |
Ixcyc |
Ic |
Iy |
Iyy |
| а) |
bh3/2 |
b3h/12 |
0 |
bh3/3 |
b3h/3 |
b2h2/4 |
| б) |
bh3/36 |
b3h/36 |
-b2h2//78 |
bh3/12 |
b3h/2 |
b2h2/24 |
| в) |
Пd4/64 |
Пd4/64 |
0 |
- |
- |
- |
| г) |
0,11r2 |
Пd/128 |
0 |
Пd4/128 |
- |
- |
|
| |
 |
| Рис. 4.5 |
| Знак центробежного момента инерции сечения часто можно определить
по чертежу сечения (рис.4.6). |
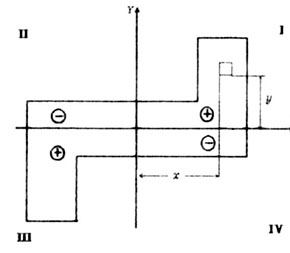 |
| Рис. 4.6 |
| Согласно формуле |
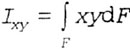 |
| Отсюда, части площади, находящиеся в I и III квадрантах,
имеют положительные центробежные моменты инерции, так как произведения координат
х и у элементарных площадок dF, находящихся в этих квадрантах дают положительные
величины. Части площади, находящиеся во II и IV квадрантах имеют отрицательные
центробежные моменты инерции. |
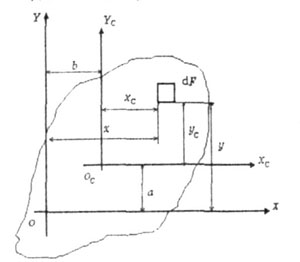
| Моменты инерции относительно параллельных осей, одни из которых
центральные (XC0CYC) опре-депяются из выражений (рис. 4.7): |
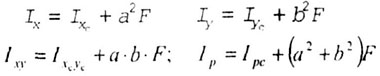 |
| где a и b - координаты центра тяжести сечения Оc |
 |
| Рис. 4.7 |
| Координаты a и b необходимо подставлять в эти формулы с учетом
их знаков. |
| Моменты инерции, входящие в формулы для определения прочности
и жесткости конструкции вычисляются относительно осей, которые являются
не только центральными, но и главными. Чтобы определить какие оси, проходящие
через центр тяжести, являются главными, надо уметь определять моменты инерции
относительно осей, повернутых относительно друг друга на некоторый угол.
|
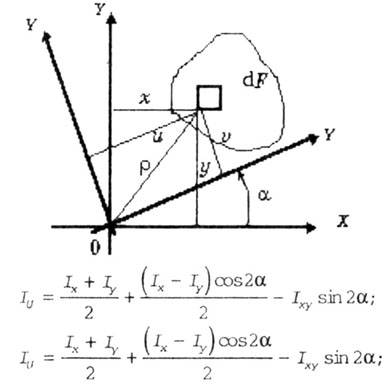
| Зависимости между моментами инерции при повороте координатных
осей (рис. 4.8) имеют вид: |
 |
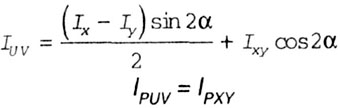 |
| Рис. 4.8 |
где 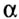 - угол между
осями XOY и UOY. Угол считается положительным, если поворот осей XOY происходит
против часовой стрелки. - угол между
осями XOY и UOY. Угол считается положительным, если поворот осей XOY происходит
против часовой стрелки. |
| Главными осями инерции называются
две взаимно перпендикулярные оси, относительно которых центробежный момент
инерции сечения равен нулю. |
| Направление главных осей инерции определяется уравнением |
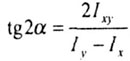 |
| Главными моментами инерции называются
осевые моменты инерции, вычисленные относительно главных осей инерции, которые
имеют экстремальные значения |
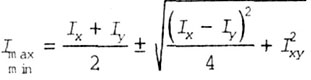 |
| Главные оси, проходящие через центр тяжести сечения, называются
главными центральными осями, а моменты инерции
относительно этих осей -главными центральными моментами инерции. |
| Ось симметрии плоского сечения является | главной центральной
осью инерции этого сечения. |
| Если плоское сечение имеет хотя бы две оси симметрии неперпендикулярные
друг другу, то все оси, проходящие через центр тяжести этой фигуры, являются
ее главными центральными осями инерции. Осевые моменты инерции площади сечения,
вычисленные относительно этих осей, равны между собой (рис. 4.9). |
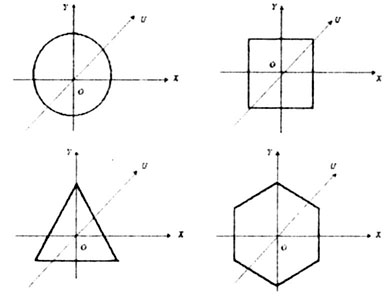 |
| Рис. 4.9 |
| Моменты инерции сложных сечений определяются по формулам |
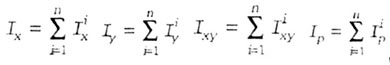 |
где 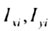 - осевые моменты
инерции; - осевые моменты
инерции;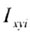 - центробежные моменты
инерции; - центробежные моменты
инерции; 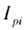 - полярные моменты инерции
отдельных фигур сечения. - полярные моменты инерции
отдельных фигур сечения. |
| |
 |