 |
| Деформации и перемещения при растяжении - сжатии. |
| |
| |
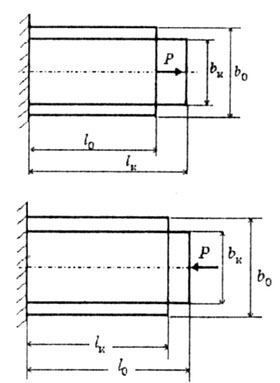
| При растяжении и сжатии бруса меняются его продольные и поперечные
размеры (рис.2.4). |
 |
| Рис. 2.4 |
| При растяжении: |
Длина бруса меняется на 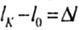 (удлинение),
(удлинение), |
Ширина бруса меняется на 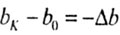 (сужение).
(сужение). |
| При сжатии: |
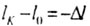 (укорочение) (укорочение) |
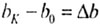 (увеличение (увеличение |
| Закон Гука выражает прямо пропорциональную
зависимость между нормальным напряжением и относительной деформацией: |
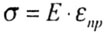 |
| или, если представить в другом виде: |
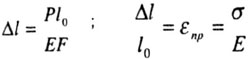 |
| где Е - модуль продольной упругости. |
| Это физическая постоянная материапа, характеризующая его
способность сопротивпяться упругому деформированию. |
| EF - жесткость поперечного сечения бруса при эастяжении-сжатии. |
| абсолютная деформация (см, м) |
относительная деформация безразмерная |
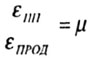
коэффициент поперечной деформации, коэффициент Пуассона
|
|  l продольная l продольная
|
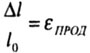
продопьная
|
|  b поперечная b поперечная
|
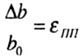
поперечная
|
|
| Деформация бруса (растяжение ипи сжатие) вызывает перемещение
поперечных сечений. |
| Рассмотрим три случая нагружения при растяжении. |
В первом случае при растяжении бруса сечение n-n перемещается
в положение n1-n1
на величину  . Здесь: перемещение
сечения равно деформации (удлинению) бруса . Здесь: перемещение
сечения равно деформации (удлинению) бруса  =
=  l. (рис.2.5). l. (рис.2.5). |
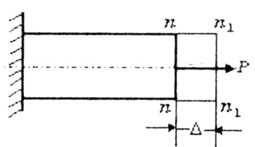 |
| Рис. 2.5 |
| Во втором случае растяжения (рис. 2.6) |
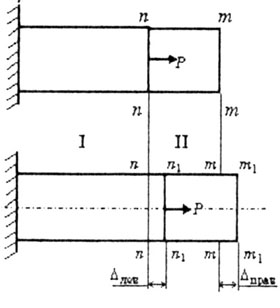 |
| Рис. 2.6 |
l-ый участок бруса деформируется (удлиняется) на величину
 l1,
сечение n-n перемещается в положение n1-n1
на величину l1,
сечение n-n перемещается в положение n1-n1
на величину  лев = лев =  l1. l1.
|
| ll-ой участок бруса не деформируется, так как здесь отсутствует
продольная сила N, сечение m-m перемещается в положение m1-m1
на величину |
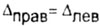 |
| В третьем случае рассмотрим деформации бруса при схеме нагружения,
представленной на рисунке (рис.2.7). |
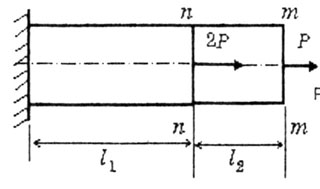 |
| Рис. 2.7 |
В этом примере: перемещение сечения n-n ( лев)
равно удлинению 1-ого участка бруса: лев)
равно удлинению 1-ого участка бруса: |
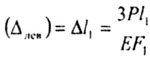 |
| Сечение m-m переместится в положение m1-m1
за счет деформации 1-ого участка бруса, а в положение m2-m2
за счет своего собственного удлинения (рис.2.8): |
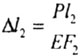 |
| Суммарное перемещение сечения m-m: |
 |
| В данном случае: |
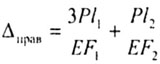 |
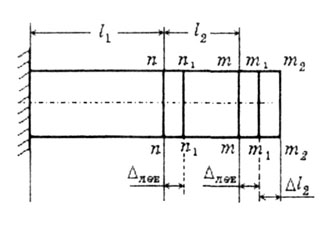 |
| Рис. 2.8 |
| С использованием эпюры N получаем такой же результат (снимаем
N с эпюры) (рис.2.9). |
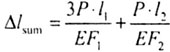 |
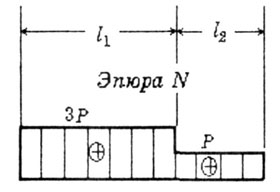 |
| Рис. 2.9 |
| Перемещение конца консоли можно получить, используя только
внешние силы (2Р,Р). Тогда: |
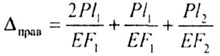 |
| |
 |