315.3. В правильной треугольной призме
ABCA1B1C1 проведено сечение через вершину
С1и ребро АB. Найдите периметр сечения. Если сторона основании
равна 24 см, а боковое ребро = 10 см.
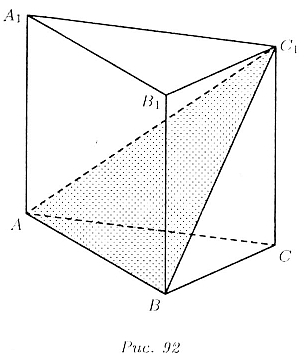
Сечение ABC1 - равнобедренный треугольник, так как
BC1 = AC1
как диагонали боковых граней (рис. 92). В правильной треугольной призме
боковые ребра перпендикулярны основанию. Поэтому треугольник BCC1
-— прямоугольный и по теореме Пифагора
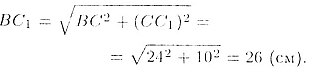
Таким образом, периметр сечения равен
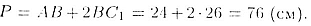
Ответ. 76 см.
315.4. Докажите, что если точка X равноудалена
от концов данного отрезка AB то она лежит па плоскости, проходящей через
середину отрезка АB и перпендикулярной прямой AB.
Пусть X -— некоторая точка пространства такая, что
AX = BХ
Через точку X п прямую Alt можно принести плоскость а (рис. 93). Известно,
что мпожество точек плоскости а, равноудаленных от концов A и B отрезка
AB, представляет собой серединный перпендикуляр ОX к oтрезку АB (О — середина
АB), т.е.
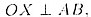
АО = BО.

Пусть теперь Y — другая точка (не лежащая на ОX) такая, что
AУ = BУ
Тогда все точки прямой OY также равноудалены от А и B. Через прямые
ОX и OY проходит единственая плоскость 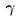 .
Для каждой точки Z, плоскости .
Для каждой точки Z, плоскости 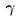 имеем
имеем
AZ = BZ
(по аналогии с предыдущим). Еcли W точка, не принадлежащая 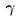 ,
то ,
то
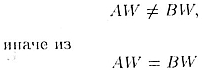
получим, что W лежит в 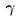 .Плоскость .Плоскость
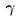 определена
по единственной точке X. Эта плоскость проходит через X и перпендикулярна
АB, Требуемое доказано. определена
по единственной точке X. Эта плоскость проходит через X и перпендикулярна
АB, Требуемое доказано.
|