34.3. Образующая конуса, наклонена
к плоскости основании под углом 30°, а его высота раина 12 см. Найдите
площадь его боковой поверхности.
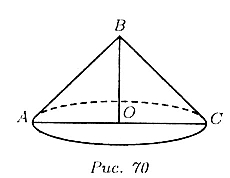
Пусть 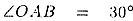 ,
OB= 12 см (рис. 70). Площадь ,
OB= 12 см (рис. 70). Площадь 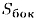 боковой
поверхности конуса вычисляется но формуле боковой
поверхности конуса вычисляется но формуле  ,
где R — радиус основания ,
где R — радиус основания 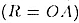 ,
L — образующая (L = АB). Из прямоугольного треугольника АОВ находим ,
L — образующая (L = АB). Из прямоугольного треугольника АОВ находим
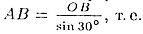
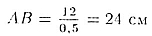
(можно было использовать свойства катета напротив угла » 30° — его длина
равна половине гипотенузы). Из того же треугольника вычислим
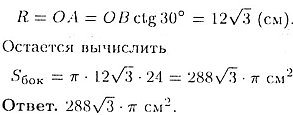
34.4. Через основание трапеции проведена
плоскость, отстоящая от другого основания на расстоянии а. Найдите расстояние
от точки пересечения диагоналей трапеции до этой плоскости, если основания
трапеции относятся как m : n.
Пусть дана трапеция AВСD, где АD : BС — m : и, О — точка пересечения диагоналей
АС и BD (рис. 71). Через АD проходит плоскость а. Высота LK трапеции проведена
через точку О, а l — прямая, лежащая в плоскости a. причем l проходит
через K' перпендикулярно АD. В плоскости, определяемой прямыми l и KL,
проведены перпендикуляры LN и OM к прямой l, т.е. 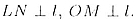
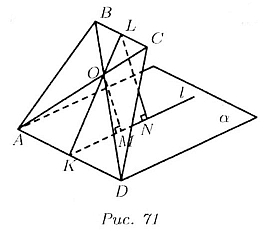
Дано, что LN = а. Требуется найти ОМ.
1 . Поскольку 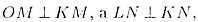 то ОМ || LN. Поэтому треугольники OKM и LKN подобны (по первому признаку:
углы одного треугольника равны соответственно углам другого треугольника).
Следовательно,
то ОМ || LN. Поэтому треугольники OKM и LKN подобны (по первому признаку:
углы одного треугольника равны соответственно углам другого треугольника).
Следовательно, 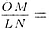 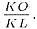
2. Треугольники АОD и COD подобны также но первому признаку: 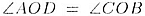 И как вертикальные
И как вертикальные 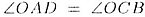 как углы накрест-лежащие при параллельных прямых
как углы накрест-лежащие при параллельных прямых 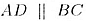 и секущей
и секущей 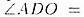 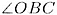 по
аналогичной причине. Следовательно, стороны этих треугольников пропорциональны.
Известно, что в подобных треугольниках пропорциональны и другие линии,
н маетности высоты. Поэтому по
аналогичной причине. Следовательно, стороны этих треугольников пропорциональны.
Известно, что в подобных треугольниках пропорциональны и другие линии,
н маетности высоты. Поэтому
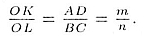
Можно считать, что
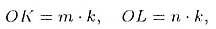
где А: — некоторый масштабный коэффициент (или коэффициент пропорциональности).
Тогда
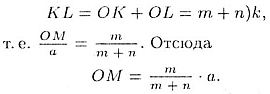
Замечания. Ответ к задаче получим другим, если принять 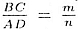 или если плоскость а провести через другое основание BС. Именно, ответ
отличается тем, что m и п меняются местами.
или если плоскость а провести через другое основание BС. Именно, ответ
отличается тем, что m и п меняются местами.
Ответ: 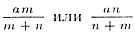
|