В одной из двух плоскостей 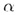 ||
|| 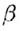 имеется замкнутая линия Z.
Фигуру, ограниченную линией Z, обозначим буквой Ф. Пусть l -- некоторая
прямая, пересекающая плоскости имеется замкнутая линия Z.
Фигуру, ограниченную линией Z, обозначим буквой Ф. Пусть l -- некоторая
прямая, пересекающая плоскости 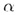 и
и 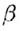 . Из точек М линии Z проводим
отрезки, параллельные l и заключенные между плоскостями . Из точек М линии Z проводим
отрезки, параллельные l и заключенные между плоскостями 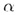 и
и 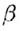 . Полученная при этом поверхность
называется цилиндрической поверхностью. . Полученная при этом поверхность
называется цилиндрической поверхностью.
К цилиндру присоединяют фигуры Ф и Ф1
(Ф1
— фигура, равная фигуре Ф и принадлежащая плоскости 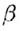 )
и все точки пространства, расположенные внутри цилиндрической поверхности
(между плоскостями). )
и все точки пространства, расположенные внутри цилиндрической поверхности
(между плоскостями).
Фигуры Ф и Ф1
называются основаниями цилиндра, Z -- направляющей цилиндра, М1
— его образующей.
Если прямая l перпендикулярна плоскости 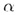 и
и 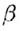 , то цилиндр называется прямым
(в противном случае — наклонным). , то цилиндр называется прямым
(в противном случае — наклонным).
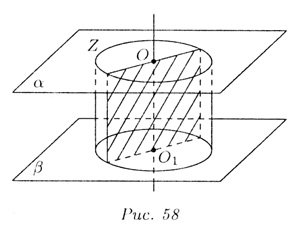
Прямой цилиндр называется круглым (круговым), если направляющая Z является
окружностью, а основания Ф и Ф1
— круги (рис. 58).
Расстояние между основаниями цилиндра называется его высотой. Прямая
ОО1,
проходящая через центр О и O1
кругов оснований, называется осью цилиндра. Сечение цилиндра плоскостью,
проходящей через его ось, называется осевым сечением. Осевое сечение цилиндра
— прямоугольник.
Предметы цилиндрического вида являются трубы, колодцы, и последнее время
появляются дома цилиндрической формы.
|