Прямая и плоскость в пространство могут:
- а) не иметь общих точек;
- б) иметь ровно одну общую точку;
- в) иметь хотя бы две общие точки.
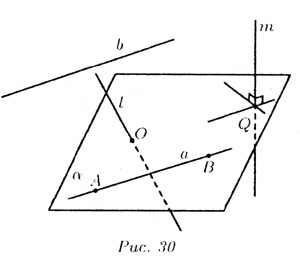
На рис. 30 изображены все эти возможности.
В случае а) прямая b параллельна плоскости :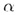
b || .
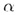В случае б) прямая l пересекает плоскость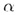
в одной точке О; l  =
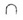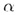О.
В случае в) прямая а принадлежит плоскости :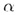
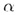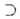а или а  .
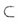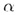Теорема. Если прямая b параллельна хотя бы
одной прямой а, принадлежащей плоско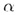сти ,
то прямая параллельна плоскости .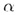
Предположим, что прямая m пересекает плоскость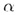
в точке Q.Если m перпендикулярна каждой прямой плоскости ,
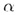проходящей через точку Q, то прямая m называется перпендикулярной к плоскости
.
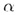Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли.
Линии электропередачи параллельны плоскости земли, а стволы деревьев могут
служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные
плоскости земли, другие — не перпендикулярные (наклонные).
|
