| 1. Последовательностью называется бесконечное занумерованное
множество действительных чисел, обозначаемое а1,
а2,...
, аn,...
, или кратко
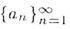
Другое определение последовательности — функция натурального аргумента.
2. Арифметическая прогрессия определяется двумя числами а (первый член)
и d (разность прогрессии) и имеет вид
а, а + d, а + 2d,.. ., а + (n — 1) d, ....
При этом
an
= а + (n — 1)d
— формула общего члена,
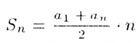
— формула суммы n первых членов арифметической прогессии,
2ак
= ак-1
+ак+1
= ак-2
+ ак+2
= ...
- свойство членов арифметической прогрессии.
3. Геометрическая прогрессия определяется двумя числами b (первый член.
b # 0) и g (знаменатель
прогрессии, g #
0, g # 1 и имеет
вид
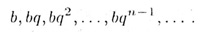
При этом
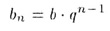
— формула общего члена,
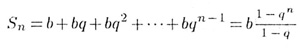
— формула суммы первых n членов,
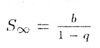
(только при |g| < 1) — формула суммы бесконечно убывающей геометрической
прогрессии;
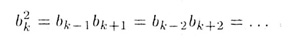
- свойство членов геомегрической прогрессии.
|