1. В прямоугольной системе координат Oхy:

2. Уравнение окружности радиуса R с центром в точке М0(x0;y0)
имеет вид
(х - x1)2
+ (y - y02)
= R2
3. Неравенство
ax + by + c > 0
определяет полуплоскость с границей ax + by + с = 0. Полуплоскость определяется
той точкой (x0;y0),
для которой ax0
+ by0+
с > 0.
4. Система уравнений
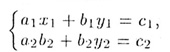
• совместна в том и только в том случае, когда
a1b2
- b2b1
# 0
• несовместна, если
a1b2
- b2b1=
0 и a1c2
- a2c1
# 0
или
b1c2
- b2c1
# 0
• имеет бесконечное множество решений, если
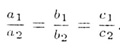
|