1. Угол (дуга) в тригонометрии измеряется в градусах и
радианах:
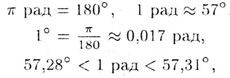
а его величина положительна или отрицательна в зависимости от того,
отсчитывается ли он от начального радиуса О А (точки A) против или по
часовой стрелке (рис. 4). Например,
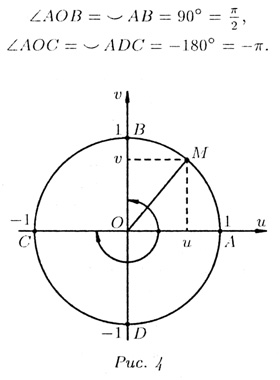
2. Единичную окружность
u2
+ v2
= 1
отнесем к прямоугольной системе координат Оuv. Каждой точке M(u;v) этой
окружности (u — абсцисса, v — ордината М) соответствует бесконечное множество
угловых (дуговых) координат:
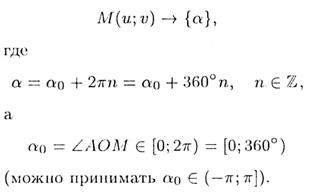
3. Тригонометрические функции синус, и косинус определяются при помощи
координат u и v точки М:
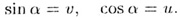
sin a = и, cos а = и.
Две другие функции — тангенс и котангенс — можно определить следующим
образом (рис. 5). Касательную At(Bт) превратим в числовую прямую с началом
в точке A(В), положительным направлением вверх (вправо) и единицей масштаба,
равной радиусу окружности. Через t(т) обозначим координату точки пересечения
прямой ОМ с осью тангенсов At (котангенсов Bт).
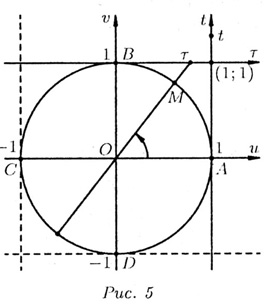
По определению, принимаем:

Если 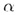 измеряется в градусах,
то говорят о функциях углового аргумента, а если в радианах — о функциях
числового или абстрактного аргумента (числовой аргумент чаще обозначают
буквой х, а угловой — буквой измеряется в градусах,
то говорят о функциях углового аргумента, а если в радианах — о функциях
числового или абстрактного аргумента (числовой аргумент чаще обозначают
буквой х, а угловой — буквой 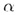 ). ).
|